http://www.mathplayground.com/ShapeMods/ShapeMods.html
CC ALG I
Tuesday, April 1, 2014
Sunday, March 30, 2014
Compound Interest
P = principal amount (the initial amount you borrow or deposit)
r = annual rate of interest (as a decimal)
t = number of years the amount is deposited or borrowed for.
A = amount of money accumulated after n years, including interest.
n = number of times the interest is compounded per year
|
Example
An amount of $1,500.00 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly. What is the balance after 6 years?
|
Solution
| Using the compound interest formula, we have that P = 1500, r = 4.3/100 = 0.043, n = 4, t = 6. Therefore, 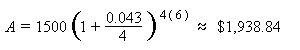
So, the balance after 6 years is approximately $1,938.84.
|
Thursday, March 20, 2014
Liner Programming
<<<Image
Goes Here>>>
|
||||||||
Vertices:
(0,6) (0,0) (6,0) |
||||||||
Constraints
|
Objective Function:
|
|||||||
|
y ≥
0
x + y ≤ 6
|
C + 3x = 4y
|
|||||||
<<<Image Goes Here>>>
|
||||||||
Vertices:
(0,6) (-5,4) (0,4) |
|
|||||||
Constraints
|
Objective Function:
|
|||||||
x ≤ 5
y ≥ 4
-2x + 5y ≤ 30
|
C = 2x + 5y
|
|||||||
|
<<<Image Goes Here>>>
|
||||||||
|
Vertices:
(1,8)
(1,2)
(5,2)
|
|
|
|
|
||||
|
Constraints
|
Objective Function:
|
|||||||
|
x ≥
0
y ≥
0
x + y ≤ 5
|
|
|
|
|
|
|||
|
<<<Image Goes Here>>>
|
||||||||
|
Vertices:
(0,8)
(0,4)
(6,8)
|
|
|
|
|
||||
|
Constraints
|
Objective Function:
|
|||||||
|
x ≥
0
y ≥ 8
-2x +3 y ≤ 12
|
|
|
|
|
|
|||
|
<<<Image Goes Here>>>
|
||||||||
|
Vertices:
(0,5)
(0,4)
(2,3)
|
|
|
|
|||||
|
Constraints
|
Objective Function:
|
|||||||
|
x ≥
0
y ≥
0
4x +4 y ≤ 20
x + 2y ≤ 8
|
|
|
|
|
|
|||
|
<<<Image Goes Here>>>
|
||||||||
|
Vertices:
(0,4)
(0,2)
(3,0)
(4,3)
|
|
|
|
|
||||
|
Constraints
|
Objective Function:
|
|||||||
|
x ≥
0
2x + 3y ≥ 6
3x - y
x +4 y ≤ 16
|
|
|
|
|
|
|||
Tuesday, March 4, 2014
Graphing Exponential Growth/Decay
Graphing Exponential Growth/Decay
- Formula: y=a*bx-h+k
- a= multiplier (greater than, vertical stretch, if a is in between o & l it"s a vertical compression, if it gets flipped)
- b= base (either a number between o &1 or greater than 1)
- h= left/right (up)
- k= up/down
- domain= (
- asmtope= (y=k) r+ range y<k when a s negative & y > k when a is positive
Negative exponents mean to FLIP A FRACTION
Tuesday, January 21, 2014
Characteristics and Traits of Graphs
Domain - Determine how far left & right the graph goes
Range - Determines how far up & down the graph goes
End Behavior - Describes the 2 ends of an equation
Absolute Max/Min - point that highest/lowest on the graph
Local Max/Min -More than one point that is the highest or lowest
Interval of increase - point where it increases the x axis
Interval of decrease - section of graphs when y values are decreasing
X intercept - point where it crosses the x axis
Y intercept - point where it crosses the y axis
Symmetry - even: symmetric at y axis
odd: symmetric at orgion
neither: no symmetry
Asymptotes - imaginary line closer & closer to the line but never touches it
Function - passes vertical line test
One to One - passes vertical & horizontal line test
Range - Determines how far up & down the graph goes
End Behavior - Describes the 2 ends of an equation
Absolute Max/Min - point that highest/lowest on the graph
Local Max/Min -More than one point that is the highest or lowest
Interval of increase - point where it increases the x axis
Interval of decrease - section of graphs when y values are decreasing
X intercept - point where it crosses the x axis
Y intercept - point where it crosses the y axis
Symmetry - even: symmetric at y axis
odd: symmetric at orgion
neither: no symmetry
Asymptotes - imaginary line closer & closer to the line but never touches it
Function - passes vertical line test
This is an example of a line failing the vertical line test so...
NOT A FUNCTION!
One to One - passes vertical & horizontal line test
Subscribe to:
Comments (Atom)








